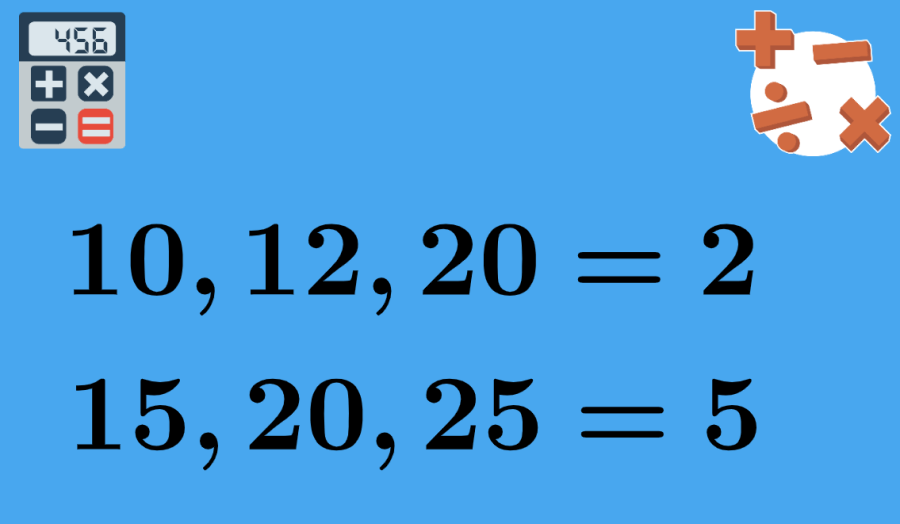What is implied by Most prominent Normal Divider?
In math, the term most noteworthy normal divisor is characterized as the biggest conceivable positive number that partitions a given number and gives zero as the rest of. The best normal divisor is otherwise called the best normal divisor, most prominent normal element (GCF), or most elevated normal component (HCF). At the point when we allude to “most noteworthy normal divisor”, the modifier “most prominent” can undoubtedly be supplanted by “most elevated”, and “divisor” can likewise be supplanted with “factor”. Subsequently, we additionally know the best normal divisor as the most noteworthy normal variable, most prominent normal component (GCF), and so forth.
TechsBoy techsboy.com
Strategy To Ascertain Gcd And Its Applications
As we have laid out, the GCD of any at least two such whole numbers will be the best number that isolates every whole number with the end goal that their leftovers are zero. Thus, there are different strategies or calculations to decide the G.C.D (Most prominent Normal Divider) between any two given numbers. In this way, on the off chance that we discuss the most straightforward and quickest cycle to compute GCF, it comprises of disintegrating every one of the given numbers as results of prime factors and afterward partitioning each number by the primes will incorporate. We arrive at a remainder that rises to 1. For instance, GCD of 20 and 30 = 10 (since 10 is the best normal number that partitions 20 and 30 and the rest of nothing).
GCD of 42, 120, and 285 = 3 (as 3 is the best normal number that separates 42, 120, and 285 and the rest of nothing).
40 of 60 https://techsboy.com/40-of-60/
How To Ascertain G.C.D?
There are different strategies or calculations to decide the G.C.D (most noteworthy normal divisor) between two given numbers. On the off chance that we discuss the most straightforward and quickest process, it includes disintegrating each number into a result of prime elements, and afterward separating each number by indivisible numbers until we get a remainder equivalent to 1. try not to reach.
To make it simpler for you to comprehend, we will examine a model. We need to decide the G.C.D somewhere in the range of 168 and 180. In the first place, we start by figuring each number as displayed beneath.
Considering in, we will presume that 168 = 2 × 2 × 2 × 3 × 7 and 180 = 2 × 2 × 3 × 3 × 5.
In the subsequent stage, we’ll decide the result of the normal elements with the more modest example: 2 × 2 × 3 = 12.
At long last, we can presume that the best normal divisor somewhere in the range of 168 and 180 is 12.
Uses Of The Best Normal Divisor
There are numerous issues where the assurance of GCD is extremely valuable. Suppose a flower specialist has 180 roses and 168 daisies, and she needs to include the groups where she can have the two kinds of blossoms (roses and daisies) with similar number of blossoms. For this situation, by establishing that G.C.D is 12, it gets the job done to do 168:12=14 and 180:12=15. Hence, it is feasible to make 12 groups, where each will contain 14 roses and 15 daisies.
Utilizations of LCM and GCD surely assist with a great deal of things.
Here are some of them:
Assists in number juggling with addressing divisions. Isn’t it? To tackle for divisions with an alternate denominator, we first put them in quite a while.
Assists with tracking down likenesses. 2*4=8; 4*2=8 too. We can utilize either 2 four times or 4 two times to get eight. In situations where you really want to appropriate, consider the possibility that similar 10 chocolates are given to five kids rather than 2.
We regularly track down the utilization of GCDs in the estimation and development areas.
Assuming we know LCM and GCD, we can find the result of numbers as it were.
What Is The G.C.D Of Two Numbers?
We, right off the bat, have proactively examined that G.C.D isn’t determined between two numbers as it were. We can likewise decide the G.C.D of 2, 3, 4 or more numbers. In this manner, assume we have two distinct regular numbers. Presently, we guarantee you that there will be shared factors between them. In the event that there is a case where there is just a single normal divisor since that divisor matches the number 1, they are supposed to be generally rudimentary numbers. Yet, on the off chance that they have different normal divisors, G.C.D will be the best of those divisors.